Singlegrid and doublegrid games
The hexgrid and its relation to the square grid
The checkered hexgrid - subgrids
One league beyond and one league behind
Alquerque and the checkered square
The draughts variants discussed here are played on boards with square or hexagonal grids. The use of these grids has varied in time and place, the hexgrid being a very recent addition to an otherwise 'square' history. Rather than taking knowledge of the boards' properties for granted, we'll first discuss the basics here, not from a historical point of view, but from a topological one.
 grids_(1) | 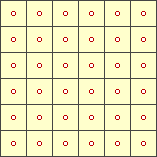 grids_(2) | 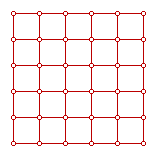 grids_(3) |
Our point of departure is a regular square grid (1). It has squares and vertices. Put a point in the center of each square (2) and connect the points (3) and you have obtained the 'dual' grid. The dual grid of a square grid is also a square grid.
A game played on the squares of (1) can also be played on the vertices of (3). Both conventions are followed in different games. The game of Go is played on vertices, as is Xiangqi, the traditional Chinese form of Chess. Draughts variants are usually played on the squares, or the 'cells' in case of a hexgame.
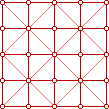 grids_(4) | 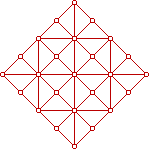 grids_(5) | 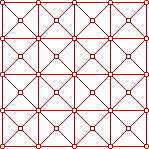 grids_(6) | However, Alquerque, the mother of all draughts variants, was played on the vertices of a square grid with one set of added diagonals (4). We hope to show this to be very significant in the evolution of draughts variants. If we rotate (4) by 45 degrees we get (5) and, squared up, (6) which is the 'Kharbaga' board. |
In (4) half the diagonals have been removed, in (6) half the straight lines, but topologically they are identical. Aren't grids fun!
The transfer from vertices to squares, according to the Dutch draughts historian Arie van der Stoep, occured in the 14th century:
"In the 14th c., draughts was transferred from the lined board to the chess board. Some civilizations played chess on unchequered boards, others on chequered boards. Where the chess board was unchequered, like in the Middle East, draughts became an orthogonal game. Where the chess board was chequered, like in France, Italy, England and Spain, draughts became a diagonal game." (source).
 grids_(7) |  grids_(8) | 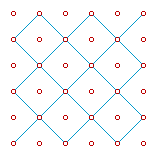 grids_(9) |
The two different approaches resulted from (1) and (7). Using only a diagonal sub-grid led to a division, not only between the 'Turkish' game and the 'European' game, but also to a diversion from the topology of the Alquerque board, that was to have significant consequences for the games' evolution. Before we get to that, let's first look at some of the implications:
- Both the straight grid and a diagonal sub-grid are square grids. You can see that in (8) and (9). If the distance between the vertices in the straight grid is 1, then the distance between the vertices in the diagonal grids is √2.
- From a vertex in grid (3) there's one forward direction, two sideways, and one backwards. From a vertex in grids (8) and (9) there are two forward directions, and two backwards.
- A diagonal sub-grid has only half the squares of the straight grid. If Draughts is magic, you can extract a lot more magic on twice the squares. Here lies the reason the main representative of the 'European' branch ended up on a 10x10 board.
- Apart from the mere number of squares, note also that in the straight grid movement and capture align with the board, allowing longer capturing sequences.
Singlegrid and doublegrid games
One aspect of this division has been underexposed: In the majority of cases the variants emerging in both branches remained restricted to either the straight grid or the diagonal grid. We will call this singlegrid games.
In the whole European/Anglo-American branch only one Dutch, or rather Frisian variant emerged in the 17th century in which straight capture was introduced in an otherwise diagonal game. Based on the then new 'Polish' game, the later 10x10 International Draughts, 'Frisian Draughts' untill recently was the only European 'doublegrid' game.
In the straight branch too, the main representative Dama, or Turkish Draughts, remained a straight singlegrid game, that is: without diagonal movement or capture.
Evolution tends to go from the simple to the more complex. In Draughts however, we seem to see the reverse where boards are concerned. The Alquerque board (4) is not a simple square, but a square with one additional set of diagonals that indeed are used as additional directions: Alquerque is a doublegrid game. It's main offspring has been split like a siamese twin into two singlegrid games: Turkish and International.
One of the Turkish's offspring, 'Armenian Draughts' evolved into a doublegrid game once again. 'Ossetian Draughts' may have retained the doublegrid character, possibly evoling directly from Alquerque. But they're outside the mainstream, as is Frisian Draughts.
One might even question whether Turkish Draughts is 'mainstream'. Its character is somewhat archaic, it suffers from a slow image due to its sideways manoeuvring and there are hardly any organised tournaments.
Meanwhile Checkers, the mother of diagonal draughts, has been solved and is waning, and International Draughts is bending under the load of its own accumulated theory, a theory that inevitably leads into the ocean of draws embedded in the game tree. Not a sea, an ocean, but that is another discussion.
A discussion however, that must have gone on in the mind of the late Ljuban Dediç, mathematician, international Draughts master and 9 times champion of the former Yugoslavia. In order to create a draughts game with a smaller margin of draws, he took a number of bold and drastic steps.
- He 'straightened out' the game, no pun intended, by taking Turkish Draughts as its basis, therewith removing the source of Draughts' drawishness, which is a long-range king on a diagonal grid. In Turkish Draughts two kings win against one: end of problem.
- After filling the vacant back rows, he replaced the sideways move of a man by a diagonally forward move, making it a doublegrid system with forced progress.
- Finally he brought the whole system under the rules and conventions of International Draughts.
Croda did become the first truly modern Draughts game by going back to its most ancient roots.
The hexgrid and its relation to the square grid
Croda is a full doublegrid game, that is it uses the square grid as well as both diagonal grids, as in (10) and (11).
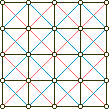 grids_(10) | 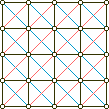 grids_(11) | 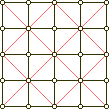 grids_(12) | 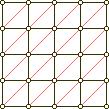 grids_(13) |
In (10) and (11) the diagonal grids are divided in a red and a blue half. Removing the blue half from each brings us to (12) and (13). In (12) we recognize the motherboard of them all, the Alquerque board. Its twin (13) is the 'triangular' grid, albeit in a square jacket. But topologically (13) is equivalent to the hexgrid:
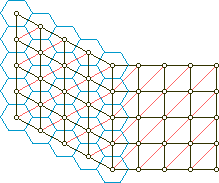 grids_(14) | 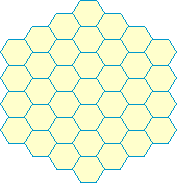 grids_(15) |
In (14) we see the square with one set of diagonals on the right. On the left it has been modelled into a grid of equilateral triangles, the 'dual' of which is the hexgrid.
The hexgrid, like its twin the 'alquerque grid', is thus equivalent with a square grid with one added set of diagonals. Games following these lines may therefore be considered partial doublegrid games.
Since the two straight directions and the one diagonal direction of (13) have become equivalent in the hexgrid (15), a game following these lines may also be considered as a singlegrid game with three forward and three backwards directions. The character of such a game however, will always be that of a partial doublegrid game.
The checkered hexgrid - subgrids
Like the square grid, the hexgrid can be checkered, but with three rather than two shades:
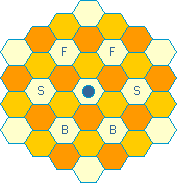 grids_(16) | 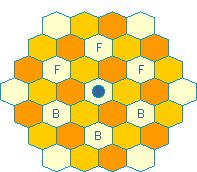 grids_(17) |
One league beyond and one league behind
Hexdame is a hexagonal i.e. partial doublegrid game in a singlegrid disguise because it uses the same grid for both movement and capture. So Hexdame may be considered a modernized draughtsgame in a logical sense. However, Draughts, in the perception of the overwhelming majority of players of whatever variants worldwide, is very much a square game, so this road's scenery, enchanting as it may be, will probably appeal only to a very small minority.
Croda is a full doublegrid game, but uses the diagonal option only for movement. Frisian is a full doublegrid game, but uses the straight option only for capture.
These games are all more or less in the same league. That's one league beyond mainstream International Draughts and one league behind Dameo. Take a good look and you can see the writing on the wall: the time of singlegrid draughts is drawing to an end. Ljuban Dedić pointed the way to save the game: a modern successor should be a doublegrid game.
